2D Parametric Collision Detection

Today I'm going to describe a method for detecting collisions between arbitrary polygons in 2D. This is part one of a two-part series, in the next post I will show how to make use of this collision detection info to do collision response.

Many collision detection methods simply test for intersection between the two polygons - but what if they are moving at high speed? What if you have a point mass that is supposed to collide with a line? In some cases testing for intersection alone will result in objects clipping through other objects - and simple intersection tests won't tell you the time of collision, the point at which collision occurred, or the normal to the surface of collision, all of which are important for proper collision response. This method will allow us to calculate all three.

Let's start by describing a parametric equation of a line passing through p₁ = (x₁, y₁) and p₂ = (x₂, y₂):

$$\vec{p} = \vec{p}_{1} + t (\vec{p}_{2} - \vec{p}_{1})$$

Or in component form:

$$x = x_{1} + t (x_{2} - x_{1})$$ $$y = y_{1} + t (y_{2} - y_{1})$$

"Parametric" in this case means that the points along the line are described by a single parameter t. When t = 0 we're at p₁ and when t = 1 we're at p₂. Any t in [0, 1] is found on the segment described by the two points, any t outside of these values is not found on the segment. Another useful property of this form is that we can describe vertical lines equally well, whereas if we were using y = mx + b we would have to special case situations with vertical lines.

When a collision occurs, it's between a point on polygon A and a line segment on polygon B, or vice versa. So if we can do collision between a moving point and a moving line, then we can easily extrapolate to collision between two moving polygons.

Consider the situation where point p₁ moves to point p₂ as time t₁ goes from 0 to 1. Line segment l₁, l₂ moves to become l₃, l₄ during the same frame.

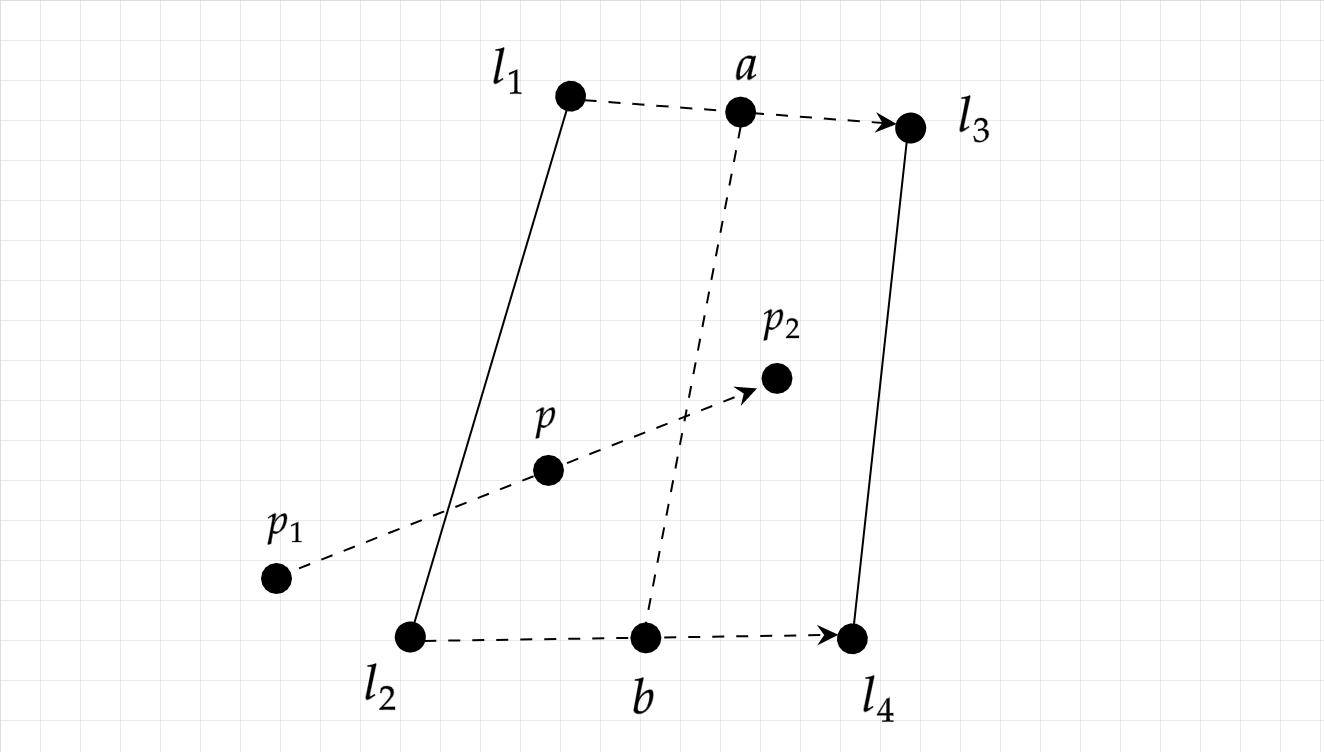
So we have p₁ going to p₂, l₁ going to l₃, and l₂ going to l₄ as t₁ goes from 0 to 1. To make notation a bit simpler I'll introduce intermediate points a and b that correspond to l₁ going to l₃ and l₂ going to l₄ respectively.

$$\vec{p} = \vec{p}_{1} + t_{1} (\vec{p}_{2} - \vec{p}_{1})$$ $$\vec{a} = \vec{l}_{1} + t_{1} (\vec{l}_{3} - \vec{l}_{1})$$ $$\vec{b} = \vec{l}_{2} + t_{1} (\vec{l}_{4} - \vec{l}_{2})$$

We have another parameter t₂ describing the line from intermediate point a to b, which may or may not intersect with the line going from p₁ to p₂.

$$\vec{p} = \vec{p}_{1} + t_{1} (\vec{p}_{2} - \vec{p}_{1}) = \vec{a} + t_{2} (\vec{b} - \vec{a})$$ $$= (\vec{l}_{1} + t_{1} (\vec{l}_{3} - \vec{l}_{1})) + t_{2} ((\vec{l}_{1} + t_{1} (\vec{l}_{3} - \vec{l}_{1})) - (\vec{l}_{2} + t_{1} (\vec{l}_{4} - \vec{l}_{2})))$$

We need to solve for the two unknowns t₁ and t₂, and luckily we have two equations once we break up the above into x and y components. There are quite a few symbols but I solved for t₂ in the equation with y-components, then subbed out t₂ in the equations with the x-components and isolated t₁. As a result we get a quadratic equation of the form at₁² + bt₁ + c = 0 where a, b, and c are the following:

$$a = (y_{l3} + y_{l2} - y_{l1} - y_{l4})(x_{p2} + x_{l2} - x_{p1} - x_{l4}) -$$ $$(y_{p2} + y_{l2} - y_{p1} - y_{l4})(x_{l3} + x_{l2} - x_{l1} - x_{l4})$$

$$b = (y_{l1} - y_{l2})(x_{p2} + x_{l2} - x_{p1} - x_{l4}) +$$ $$(x_{p1} - x_{l2})(y_{l3} + y_{l2} - y_{l1} - y_{l4}) -$$ $$(y_{p1} - y_{l2})(x_{l3} + x_{l2} - x_{l1} - x_{l4}) -$$ $$(x_{l1} - x_{l2})(y_{p2} + y_{l2} - y_{p1} - y_{l4})$$

$$c = (y_{l1} - y_{l2})(x_{p1} - x_{l2}) -$$ $$(y_{p1} - y_{l2})(x_{l1} - x_{l2})$$

$$t_{1} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

If we solve the quadratic equation for t₁ we will get 0, 1, or 2 solutions. We only care about the smallest solution that is between 0 and 1 inclusive such that t₂ is also between 0 and 1 inclusive. If there is no such solution for t₁, we are done, because there was no collision in the time frame we're considering.

So for each solution between 0 and 1 for t₁, we have to go back and solve for t₂ to confirm that t₂ is also between 0 and 1 - that is, we have to confirm that the collision between the point and the line actually occurred on the segment and not elsewhere on the line.

$$t_{2} = \frac{(\vec{p}_{1} + t_{1} (\vec{p}_{2} - \vec{p}_{1})) - (\vec{l}_{1} + t_{1} (\vec{l}_{3} - \vec{l}_{1}))}{(\vec{l}_{1} + t_{1} (\vec{l}_{3} - \vec{l}_{1})) - (\vec{l}_{2} + t_{1} (\vec{l}_{4} - \vec{l}_{2}))}$$

For simplicity I have shown this as a vector equation, but you need to use either all x or all y components to solve for t₂ - and before attempting to solve you will need to check that the denominator is not zero. The denominator will be nonzero for either x or y components as long as the line segment's length was nonzero at the time of collision. And if the line segment did have zero length, we will say that once again this is evidence of no collision and stop the process here.

So now we know collision occurred between the moving point and the moving line segment at time t₁, and we can solve for the point of collision with the original parametric equation of a line:

$$\vec{p} = \vec{p}_{1} + t_{1} (\vec{p}_{2} - \vec{p}_{1})$$

To extrapolate this to finding the first collision between polygons A and B, we can just run this algorithm for each point in A and each line segment in B, and vice versa. Keeping track of the time of collision we can find the earliest collision, the point at which collision occurred, and the normal of the line segment where we collided which will be used to apply an impulse force. We can rewind time by 1 - t₁ multiplied by the real time between frames in order to prevent intersection between the polygons, and from there we can calculate an impulse force and do collision response.

Demo

You can drag around the start/end points for the point-line collision detection while this demo animates from t₁ from 0 to 1 and uses the above equations to check for collisions.

Drawbacks

Depending on how many objects you have and how frequently they collide, this method for detecting collisions may be too computationally expensive. If we have n points on polygon A and m points on polygon B we will end up having O(nm) quadratic equations to solve, in addition to all the other computation that goes into checking point-line collision. A basic intersection test would also be O(nm) but the constant factor for this method I would expect to be much higher.

Beyond computational complexity, using this method I have approximated rotation of the polygons as straight-line movement of individual points. If your polygon rotates completely once per frame but has no translational velocity, there would be no perceived movement from p₁ to p₂! So this only works if the objects aren't rapidly rotating. If they are, you would need to use more complex parametric equations to represent movement of the points and line segments, which I have not done here.