Moments of Inertia for Triangles and other Polygons
In my previous two articles I discussed collision detection and response between rigid bodies. In order to do proper collision response between rotating objects, we needed to calculate the moment of inertia about their center of mass. Here I'm going to describe how to get the moment of inertia for an arbitrary triangle, and then I'll show a triangulation algorithm to apply this to any polygon.
Right Triangles
The first step is going to be calculating the moment of inertia for a right triangle, since we can get a simple closed formula. Let's define the right triangle as having a width w and a height h, rotating about the origin with a uniformly distributed mass of density ρ. We know the area is equal to wh/2 so we can calculate the density if we only have the mass.
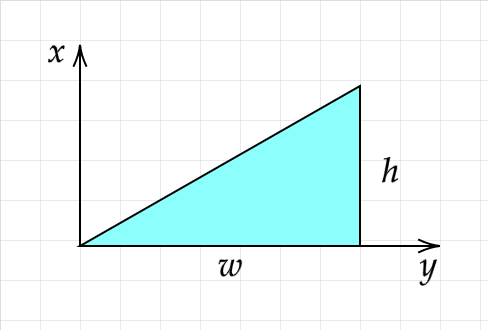
There is a great YouTube video that walks you through calculating the moment of inertia for a similar triangle, so you can watch that for a more in-depth derivation. In brief, for our right triangle we have:
$$I = \int r^2 dm = \int \int (x^2 + y^2) \rho dx dy = \rho\int_{0}^{w} dx \int_{0}^{\frac{hx}{w}} (x^2 + y^2) dy$$ $$= \rho\int_{0}^{w} dx [(yx^2 + \frac{y^3}{3})]_{0}^{\frac{hx}{w}} = \rho\int_{0}^{w} dx (\frac{hx^3}{w} + \frac{h^3x^3}{3w^3})$$ $$= \rho [\frac{hx^4}{4w} + \frac{h^3x^4}{12w^3}]_{0}^{w} = \rho(\frac{hw^3}{4} + \frac{h^3w}{12})$$
Since we are going to be rotating our triangles about their center of mass (or centroid, since the mass is uniformly distributed) we need to use the parallel axis theorem to calculate moment of inertia at the center of mass. For a triangle we can simply average the coordinates of all three points to get the centroid, and then to get the moment of inertia about the center of mass we'd do:
$$I = I_{cm} + md^2$$ $$I_{cm} = I - md^2$$
Since we're not using coordinate points yet we won't continue along this line, but we'll use it in the next section to get the moment of inertia for any triangle.
Every other triangle is just two right triangles in a trench coat
The way we will get the moment of inertia for any triangle is to split it up into two right triangles, which is very simple. Let our triangle be formed from three arbitrary points p1, p2, and p3. In this case we'll take the edge between p1 and p2 as the base, so it has length w. We can get the height by defining two vectors, v1 = p2 - p1 and v2 = p3 - p1, then getting the area of the triangle by getting their cross product and dividing by two. Since A = wh/2 we can get the height:
$$A = \frac{|\vec{v_1} \times \vec{v_2}|}{2} = \frac{wh}{2}$$ $$h = \frac{2A}{w} = \frac{|\vec{v_1} \times \vec{v_2}|}{h}$$
The situation so far with all known quantities is pictured below.
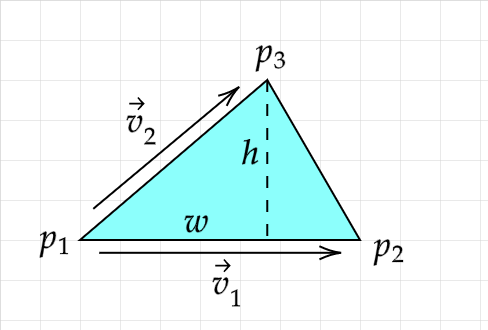
As you can see the triangle is split into two right triangles already by the dotted line representing the height. If we could find the point which we'll call p4 we could split the width w into parts w1 and w2 from which we could calculate the moments of inertia for the right triangle parts. We can use vector projection to project v2 onto v1, then add to p1 to get the coordinates for this point p4.
$$\vec{p_4} = \vec{p_1} + proj_{\vec{v_2}}\vec{v_1} = \vec{p_1} + \frac{\vec{v_2} \cdot \vec{v_1}}{\|\vec{v_1}\|^2}\vec{v_1} = \vec{p_1} + \frac{\vec{v_2} \cdot \vec{v_1}}{w^2}\vec{v_1}$$
We can then consider the distance between p1 and p4 to be w1, and the distance between p4 and p2 to be w2. We'll consider the two right triangles to be rotating around point p3 so that we can use the equation we previously derived for moment of inertia of a right triangle.
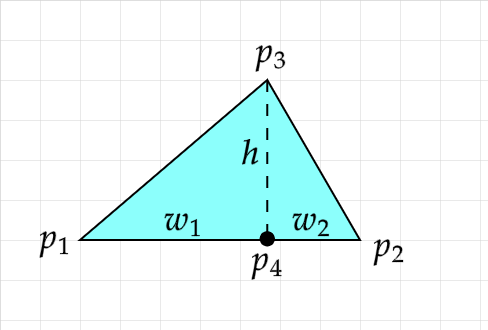
The moment of inertia for the whole triangle rotating about p3 is the sum of the moments of inertia of the two right triangle halves rotating about p3. Using the density ρ we get the following for the whole triangle:
$$I = I_1 + I_2 = \rho(\frac{hw_1^3}{4} + \frac{h^3w_1}{12}) + \rho(\frac{hw_2^3}{4} + \frac{h^3w_2}{12})$$
Then of course we can use the parallel axis theorem described in the previous section to get the moment of inertia about the center of mass. But there's one glaring problem with our formula and definition of p4. I've conveniently made the triangle in the illustrations with the longest side between p1 and p2, so we always have p4 actually on the triangle. But consider other triangle shapes:
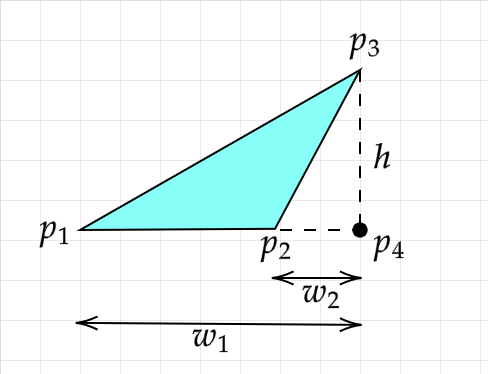
For the above, with the formula we have so far, we're going to be considering mass to exist in the empty space in triangle p2-p4-p3 twice! One thing we could do is simply rotate the labeling of the points until the longest side is between points p1 and p2. However, another solution is to check the "handedness" of each triangle and either add or subtract the moment of inertia from the total.
In the above example we will end up calculating the moment of inertia for the empty space once for a "right-handed" triangle and once for a "left-handed" triangle. These will cancel each other out if we check for handedness and we'll be left with only the moment of inertia for the original triangle. Notice that the points for right triangle p1-p3-p4 are clockwise, while the points for right triangle p2-p4-p3 are counterclockwise. In the example with no empty space, you can check that both sets of three points are clockwise.
You can check this "handedness" by checking if the cross product of two vectors along the edge of the triangle is positive or negative. You can choose whatever convention you want for which sign causes you to add or subtract from the total moment of inertia. Just remember to take the absolute value once you have the moment of inertia for the whole shape before plugging into any physics equations! And be careful about the ordering of points - order is important when calculating cross products. For the above example we have:
$$(\vec{p_4} - \vec{p_1}) \times (\vec{p_3} - \vec{p_1}) > 0$$ $$(\vec{p_3} - \vec{p_2}) \times (\vec{p_4} - \vec{p_2}) < 0$$
So the total moment of inertia I for the triangle rotating about point p3 is:
$$I = |I_1 + (-I_2)|$$
We can then get the centroid for the original triangle and get the moment of inertia about the center of mass with the parallel axis theorem, or do whatever else we have in mind for the moment of inertia.
From Triangles to Polygons
Now that we can calculate the moment of inertia for an arbitrary triangle, we can do the same for a polygon - by splitting it up into triangles. This part actually ends up being pretty simple, provided your polygon is not self-intersecting. If any two edges of the polygon intersect with each other, you'll need to fix that before applying this triangulation algorithm.
Let our polygon be composed of n points p1, p2, ... pn. We can simply let p1 be an anchor point and sum the moments of inertia for triangles with points p1, pi, pi+1 for i from 2 to n - 1. I'll illustrate this below with a few examples.
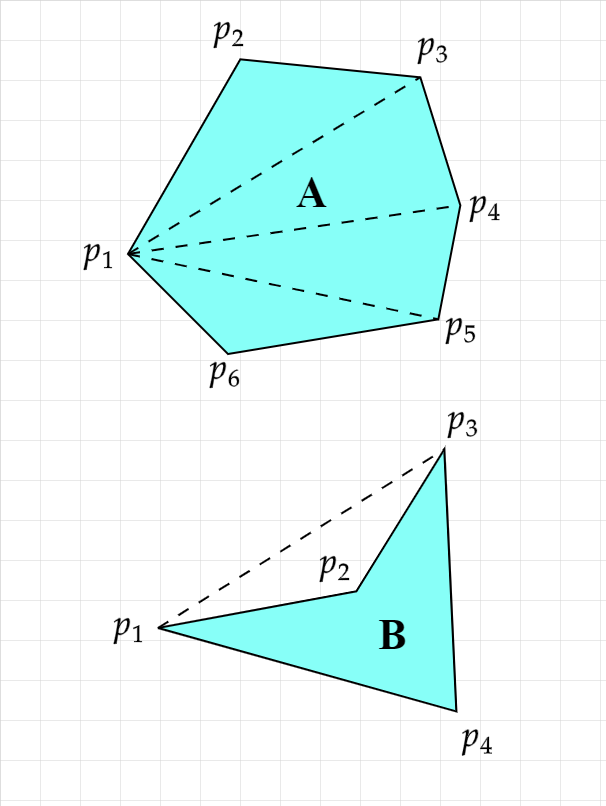
Polygon A is convex, and you can see it easily splits into triangles that are all positive space. You could just get the moment of inertia for each of the triangles, use the parallel axis theorem to change the axis to the center of mass of the polygon, then sum the results.
Polygon B however is concave, and it splits into one triangle of negative space and one triangle that is a combination of both positive and negative space. You can use the cross product as the same handedness test that we did for the triangle pieces in the last section to tell if the triangle should contribute positively or negatively to the polygon's moment of inertia. For B you end up subtracting the negative space's contribution to the moment of inertia, then adding it back, leading to a zero net contribution from the negative space.
Here's some JavaScript code of the algorithm for computing moment of inertia of a polygon with the origin as the center of mass:
function sub(p1, p2) {
return {x: p1.x - p2.x, y: p1.y - p2.y};
}
function add(p1, p2) {
return {x: p1.x + p2.x, y: p1.y + p2.y};
}
function mul(p, f) {
return {x: p.x * f, y: p.y * f};
}
function dot(p1, p2) {
return p1.x * p2.x + p1.y * p2.y;
}
function cross(p1, p2) {
return p1.x * p2.y - p2.x * p1.y;
}
function dist(p1, p2) {
p2 = p2 || {x: 0, y: 0};
const x = p1.x - p2.x, y = p1.y - p2.y;
return Math.sqrt(x * x + y * y);
}
function calcMomentOfInertia(points, density) {
let momentOfInertia = 0;
for (let i = 1; i < points.length - 1; i++) {
const p1 = points[0], p2 = points[i], p3 = points[i + 1];
const w = dist(p1, p2);
const w1 = Math.abs(dot(sub(p1, p2), sub(p3, p2)) / w);
const w2 = Math.abs(w - w1);
const signedTriArea = cross(sub(p3, p1), sub(p2, p1)) / 2;
const h = 2 * Math.abs(signedTriArea) / w;
const p4 = add(p2, mul(sub(p1, p2), w1 / w));
const cm1 = {
x: (p2.x + p3.x + p4.x) / 3,
y: (p2.y + p3.y + p4.y) / 3,
};
const cm2 = {
x: (p1.x + p3.x + p4.x) / 3,
y: (p1.y + p3.y + p4.y) / 3,
};
const I1 = density * w1 * h * ((h * h / 4) + (w1 * w1 / 12));
const I2 = density * w2 * h * ((h * h / 4) + (w2 * w2 / 12));
const m1 = 0.5 * w1 * h * density;
const m2 = 0.5 * w2 * h * density;
const I1cm = I1 - (m1 * Math.pow(dist(cm1, p3), 2));
const I2cm = I2 - (m2 * Math.pow(dist(cm2, p3), 2));
const momentOfInertiaPart1 = I1cm + (m1 * Math.pow(dist(cm1), 2));
const momentOfInertiaPart2 = I2cm + (m2 * Math.pow(dist(cm2), 2));
if (cross(sub(p1, p3), sub(p4, p3)) > 0) {
momentOfInertia += momentOfInertiaPart1;
} else {
momentOfInertia -= momentOfInertiaPart1;
}
if (cross(sub(p4, p3), sub(p2, p3)) > 0) {
momentOfInertia += momentOfInertiaPart2;
} else {
momentOfInertia -= momentOfInertiaPart2;
}
}
return Math.abs(momentOfInertia);
}
Getting Density from Mass
If you started with just the mass of your object and you don't know the density, you can calculate the area using the same triangulation formula before doing any moment of inertia calculations. The following JavaScript code will get you the area, then you can divide the mass by this area to get the density.
function sub(p1, p2) {
return {x: p1.x - p2.x, y: p1.y - p2.y;};
}
function cross(p1, p2) {
return p1.x * p2.y - p2.x * p1.y;
}
function calcArea(points) {
let area = 0;
for (let i = 1; i < points.length - 1; i++) {
const v1 = sub(points[i+1], points[0]);
const v2 = sub(points[i], points[0]);
area += cross(v1, v2) / 2;
}
return Math.abs(area);
}